初中蒟蒻对于定积分的一些看法(基础篇)
Velleity
·
2025-10-01 20:49:31
·
算法·理论
蒟蒻刚学了一些定积分的基础,觉得理解得挺通俗易懂,可以帮助同样想了解定积分却无能为力的初中生,已精通积分的大佬轻喷。
先看一张图:
这个三角形 ABC 的面积小学生都会算,它的面积 S=\frac{1}{2}ah=\frac{1}{2}\times AB\times BC=\frac{1}{2}\times2\times2=2,那么下面那个在函数 \operatorname{f}(x)=x+\frac{1}{2} 上的梯形呢?
也十分简单,它的面积 S=\frac{1}{2}(a+b)h=\frac{1}{2}\times(AB+CD)\times BC=\frac{1}{2}\times(0.5+2.5)\times2=3。那么,还有什么可以计算它的面积的方法吗?有,叫切割,如下图:
我们把横轴上 0 到 2 的区间分成了两段,每段的长度记为 \Delta x,则 \Delta x=1,再以 \Delta x 为宽构造两个矩形,长分别为 x=0 时的函数值 \operatorname{f}(0) 即 0.5,x=1 时的函数值 \operatorname{f}(1) 即 1.5。则根据矩形的面积公式,这两个矩形的面积和为 \operatorname{f}(0)\Delta x+\operatorname{f}(1)\Delta x,也就是 2,如果再分的细点呢?
不难发现,这时我们把横轴上 0 到 2 的区间分成了四段,也就是 \Delta x=0.5,那么这四个矩形的面积和就是 \operatorname{f}(0)\Delta x+\operatorname{f}(0.5)\Delta x+\operatorname{f}(1)\Delta x+\operatorname{f}(1.5)\Delta x,也就是 2.5,为了方便可观,把 0 替换成 x_0,把 0.5 替换成 x_1,以此类推。所以,这四个矩形的面积和可以表示为 \operatorname{f}(x_0)\Delta x+\operatorname{f}(x_1)\Delta x+\operatorname{f}(x_2)\Delta x+\operatorname{f}(x_3)\Delta x,这还可以简化成求和公式,即 \sum\limits_{i=0}^3\operatorname{f}(x_i)\Delta x,其中 \sum 代表求和,这整个式子的意思是从 \operatorname{f}(x_0)\Delta x 加到 \operatorname{f}(x_3)\Delta x 的和。不难发现,如果我们把横轴上 0 到 2 的区间分成了 n 段,这 n 个矩形的面积和将无限趋近于刚才那个梯形的面积,即 S\approx\sum\limits_{i=0}^{n-1}\operatorname{f}(x_i)\Delta x。
定积分的定义
那么怎么让刚才的近似值转化为精确值呢?取极限。
首先,肯定有人问:主播主播,什么是极限?
什么是极限?
极限就是,当某个量无限趋近于一个值时,这个量就会稳定奔向这个值。不理解?举个很形象的例子:你有一杯水,不停地往里加糖(\text{糖}\to\infty),这杯水的甜度(糖的浓度)就会无限趋近于一杯纯糖浆。如果用数学来描述,就是 \lim\limits_{\text{糖}\to\infty}\text{水}=\text{糖浆}。举一反三,\lim\limits_{\text{肉馅}\to0}\text{包子}=\text{馒头},理解了吗?但要注意无限趋近不等于替换,它们有本质上的区别,这确保了数学的严谨性。
例题:求 \lim\limits_{x\to0}\frac{\sin(2x)}{x}。
解析:有一个重要结论 \lim\limits_{u\to0}\frac{\sin u}{u}=1,相信各位也能自己推出来,所以对原式进行变形得:
\lim\limits_{x\to0}\frac{\sin(2x)}{x}=2\cdot\lim\limits_{x\to0}\frac{\sin(2x)}{2x}=2\cdot1=2
回到正题,如果明白了极限,就可以很容易地发现规律,我们可以直接将上文我们推出来的公式 S\approx\sum\limits_{i=0}^{n-1}\operatorname{f}(x_i)\Delta x 转化为 S=\lim\limits_{n\to\infty}\sum\limits_{i=0}^{n-1}\operatorname{f}(x_i)\Delta x,约等于变成等于了!
然后,本文章的正题终于来了,定积分,它是怎么定义的呢?你以为上文用取极限表示出来的梯形面积式子没用吗?请看下面:
\int_0^2\operatorname{f}(x)dx=\lim_{n\to\infty}\sum\limits_{i=0}^{n-1}\operatorname{f}(x_i)\Delta x
那么里面那个“撬棍”是什么?我会一一讲解。
定积分的符号
首先,那个长得像撬棍的 \int 叫积分符号,代表求和,类似于 \sum,下面的那个 0 叫积分下限,也就是刚才那个 0 到 2 的区间的左端点,这个被撬上天的 2 叫积分上限,也就是区间的右端点,[0,2] 叫积分区间,\operatorname{f} 叫被积函数,x 叫积分变量,\operatorname{f}(x)dx 叫被积表达式。
连接“面积”与“求导”的桥梁:微积分基本定理
现在我们有了表示面积的精确工具,定积分。但一个新的问题出现了:如果每个面积都要用取极限的方法去计算,那也太复杂了!我们迫切需要一种更简单的方法。
数学家们同样被这个问题困扰,直到他们发现了微积分基本定理。这个定理是微积分学的核心,它惊人地揭示了“求面积”(定积分)和“求变化率”(求导)这两个看似完全不相关的概念,其实是同一枚硬币的两面。
定理的直观理解
让我们回到那个求 \operatorname{f}(x)=x+\frac{1}{2} 在区间 [0,2] 下面积的问题。
定义一个“面积累加函数”:我们不只是想知道从 0 到 2 的总面积,我们定义一个函数 \operatorname{F}(x),它表示从起点 0 到任意一点 x 所累积的面积。例如 \operatorname{F}(0) 就表示 0 到 0 的面积也就是 0,\operatorname{F}(1) 是 0 到 1 的面积,而 \operatorname{F}(2) 就是我们想求的数。
思考:现在思考一下,当你从 x 点向右移动一点点 \Delta x,这个新增加的小长条面积 \Delta F 是多少?这个小长条的面积就近似于 \operatorname{f}(x)\Delta x,所以,面积 \operatorname{F}(x) 在 x 点的瞬时变化率就是 \frac{\Delta F}{\Delta x}\approx\operatorname{f}(x)。当 \Delta x 无限趋近于 0 时,我们就得到 \operatorname{F'}(x)=\operatorname{f}(x)(\operatorname{F'}(x) 表示 \operatorname{F}(x) 的导数,也就是它的瞬时变化率,下文会讲),也就是说,也就是说,这个“面积累加函数”\operatorname{F}(x) 的导数,恰好就是曲线本身的函数 \operatorname{f}(x)!
定理的表述
微积分基本定理告诉我们:
如果函数 \operatorname{f}(x) 在区间 [a,b] 上连续,并且 \operatorname{F}(x) 是 \operatorname{f}(x) 的一个原函数(即 \operatorname{F'}(x)=\operatorname{f}(x)),那么:
\int_a^b\operatorname{f}(x)dx=\operatorname{F}(b)-\operatorname{F}(a)
怎么求定积分?
相信通过上面的学习,你已经对定积分有大概的认识了,那么怎么求出它的值呢?要求原函数,也就是求导的逆运算。
肯定又有人问:主播主播,什么是求导?
这是一个大难点,如果弄懂了这个,定积分你也就弄懂了。
什么是求导?
首先想象一下你在骑自行车。如果你用 1 小时骑了 15 公里,你的平均速度是 15\text{公里}/\text{小时}。这就像数学中的平均变化率,看的是一段路程内的总体情况。但在你骑行过程中,速度表指针时刻在变动,比如某瞬间指向 18\text{公里}/\text{小时}。这个某一刻的速度,就是瞬时变化率。
在数学里,导数就是函数在某一点的瞬时变化率。它的几何意义是函数图像在该点的切线斜率。
当对于直线时,由于斜率是固定值。比如函数 y=2x+1,无论看哪一点,它的斜率都是 2。所以,它的导数就是 2。
但对于曲线时,曲线上不同点的切线斜率各不相同。导数就是帮助我们找出曲线上任意一点切线斜率的工具。
直接求导很麻烦,但有一些现成的规律可以背诵,让你求导更容易。
求导的基本规则
函数类型
示例
导数
简单理解
常数函数
y=5
y'=0
数值固定不变,变化率为 0。
幂函数
y=x^3
y'=3x^2
指前系数,幂减 1。
正弦函数
y=\sin x
y'=\cos x
正弦函数的变化率是余弦函数。
余弦函数
y=\cos x
y'=-\sin x
余弦函数的变化率是负的正弦函数。
指数函数
y=e^x
y'=e^x
自然指数函数的变化率是它本身。
其中 e 是自然常数,等于 \lim\limits_{n\to\infty}(1+\frac{1}{n})^n,约等于 2.71828,较为特殊。
而 \sin 则表示直角三角形中锐角对边长度与斜边长度之比,\cos 表示直角三角形中锐角邻边长度与斜边长度之比,如下图:
---
### 运算规则
- 加减法:$(u\pm v)'=u'\pm v'$。
- 乘法:$(uv)'=u'v+uv'$。(前导后不导,后导前不导)
- 除法:$(\frac{u}{v})'=\frac{u'v-uv'}{v^2}$。
- 链式法则(复合函数):$[\operatorname{f}(\operatorname{g}(x))]'=\operatorname{f'}(\operatorname{g}(x))\operatorname{g'}(x)$。(从内向外层层求导)
---
### 求导的步骤
1. **求差值**:计算函数值的改变量 $\Delta y=\operatorname{f}(x+\Delta x)-\operatorname{f}(x)$。
2. **算比值**:计算平均变化率 $\frac{\Delta y}{\Delta x}$。
3. **取极限**:让 $\Delta x$ 无限趋近于 $0$,求平均变化率的极限值。
例题:求 $y=3x^3+2x-5$ 的导数
解析:因为 $(3x^3)'=3\times3x^2=9x^2,(2x)'=2,(-5)'=0$。所以导数 $y'=9x^2+2$。
---
好的,我们又回来了。如果你理解了求导,你就可以求定积分了。这里的关键在于,**积分是求导的逆运算**。这意味着,如果我们能找到一个函数 $\operatorname{F}(x)$,使得它的导数 $\operatorname{F'}(x)$ 刚好等于被积函数 $\operatorname{f}(x)$,那么 $\operatorname{F}(x)$ 就叫做 $\operatorname{f}(x)$ 的原函数,而定积分 $\int_0^2\operatorname{f}(x)dx$ 就等于 $\operatorname{F}(2)-\operatorname{F}(0)$。
对于幂函数,求原函数有一个很好的规律,比如对 $x$ 求积分(相当于找谁的导数是 $x$),我们可以让它幂次升高一级,再从系数上进行调整。因为 $(\frac{1}{2}x^2)'=x$,所以 $x$ 的原函数之一就是 $\frac{1}{2}x^2$。同样,常数 $\frac{1}{2}$ 可以看作是 $\frac{1}{2}x^0$,它的原函数是 $\frac{1}{2}x$。
所以,$\int_0^2(x+\frac{1}{2})dx$ 的原函数就是 $\frac{1}{2}x^2+\frac{1}{2}x$,那么 $\int_0^2\operatorname{f}(x)dx$ 的结果是 $(\frac{1}{2}x^2+\frac{1}{2}x)\big|_0^2$,后面的那根竖棍意思是把上面的数字带入前面的式子得到一个值,再将下面那个数字带入前面的式子得到一个值,最终计算这两个值的差。
所以最终的计算过程是:
$$
\int_0^2\operatorname{f}(x)dx=\int_0^2(x+\frac{1}{2})dx=(\frac{1}{2}x^2+\frac{1}{2}x)\bigg|_0^2=(\frac{1}{2}\times2^2+\frac{1}{2}\times2)-(\frac{1}{2}\times0^2+\frac{1}{2}\times0)=3-0=3
$$
就是一开始那个梯形的面积。
在做题之前,定积分入门阶段有两个常用技巧,先补充一下:
方法一:**换元法**。还记得我们用“切矩形”来逼近面积吗?有时候,函数长得太复杂,直接切矩形不好算。换元法的核心思想就是:通过一次聪明的变量替换,把复杂的积分变成一个我们认识的、简单的积分。具体步骤如下:
1. 观察:在被积表达式中,寻找“一部分是另一部分的导数”这种结构,令 $u$ 为“那另一部分”。
2. 替换:然后将原积分中所有的 $x$ 用 $u$ 表示,同时把原积分的上下限替换为 $u$ 的上下限。
3. 计算新积分:算这个关于 $u$ 的简单形式的积分 $\int_{u\text{的下限}}^{u\text{的上限}}(\text{关于}u\text{的表达式})du$,求出的值即为答案。
方法二:**分部积分法**。当围成面积的曲线是两个不同类型函数相乘时,就需要这个方法。它来源于导数的计算法则 $(uv)'=u'v+uv'$。经过整理,得到:
$$
\int_a^budv=(uv)\bigg|_a^b-\int_a^bvdu
$$
那如何使用呢?当被积函数是以下五类函数中某两类相乘时,按这个优先顺序选为 $u$:
$$
\text{反三角函数}>\text{对数函数}>\text{幂函数}>\text{三角函数}>\text{指数函数}
$$
# 做题巩固
例一:对于函数 $\operatorname{f}(x)=3x^2-4x+1$,求 $\int_0^2\operatorname{f}(x)dx$。
$$
\int_0^2\operatorname{f}(x)dx=\int_0^2(3x^2-4x+1)dx=(x^3-2x^2+x)\bigg|_0^2=(2^3-2\times2^2+2)-(0^3-2\times0^2+0)=2-0=2
$$
例二:对于函数 $\operatorname{f}(x)=2\sin x+\cos x$,求 $\int_0^\pi\operatorname{f}(x)dx$。
$$
\int_0^\pi\operatorname{f}(x)dx=\int_0^\pi(2\sin x+\cos x)dx=(-2\cos x+\sin x)\bigg|_0^\pi=(-2\cos\pi+\sin\pi)-(-2\cos0+\sin0)=2-(-2)=4
$$
例三:对于函数 $\operatorname{f}(x)=2e^x-3$,求 $\int_0^1\operatorname{f}(x)dx$。
$$
\int_0^1\operatorname{f}(x)dx=\int_0^1(2e^x-3)dx=(2e^x-3x)\bigg|_0^1=(2e^1-3\times1)-(2e^0-3\times0)=(2e-3)-(2-0)=2e-3-2=2e-5
$$
例四:对于函数 $\operatorname{f}(x)=\sin(2x)$,求 $\int_0^\frac{\pi}{2}\operatorname{f}(x)dx$。
$$
\int_0^\frac{\pi}{2}\operatorname{f}(x)dx=\int_0^\frac{\pi}{2}\sin(2x)dx=[-\frac{1}{2}\cos(2x)]\bigg|_0^\frac{\pi}{2}=-\frac{1}{2}\cos(2\times\frac{\pi}{2})-[-\frac{1}{2}\cos(2\times0)]=-\frac{1}{2}\cos\pi+\frac{1}{2}\cos0=\frac{1}{2}+\frac{1}{2}=1
$$
思考题一:对于函数 $\operatorname{f}(x)=x^2+2xe^{x^2}$,求 $\int_0^1\operatorname{f}(x)dx$。
$$
\int_0^1\operatorname{f}(x)dx=\int_0^1(x^2+2xe^{x^2})dx=\int_0^1x^2dx+\int_0^12xe^{x^2}
$$
对于 $\int_0^1x^2dx$,直接求即可:
$$
\int_0^1x^2dx=(\frac{1}{3}x^3)\bigg|_0^1=\frac{1}{3}(1^3-0^3)=\frac{1}{3}\times1=\frac{1}{3}
$$
对于 $\int_0^12xe^{x^2}$,显然换元法,令 $u=x^2$,则 $du=2xdx$,原积分化为:
$$
\int_0^12xe^{x^2}=\int_0^1e^udu=(e^u)\bigg|_0^1=e^1-e^0=e-1
$$
所以最终结果为:
$$
\frac{1}{3}+e-1=e-\frac{2}{3}
$$
思考题二:对于函数 $\operatorname{f}(x)=x^3+\sqrt{1-x^2}$,求 $\int_0^1\operatorname{f}(x)dx$。
$$
\int_0^1\operatorname{f}(x)dx=\int_0^1(x^3+\sqrt{1-x^2})dx=\int_0^1x^3dx+\int_0^1\sqrt{1-x^2}dx
$$
对于 $\int_0^1x^3dx$,直接求即可:
$$
\int_0^1x^3dx=(\frac{1}{4}x^4)\bigg|_0^1=\frac{1}{4}(1^4-0^4)=\frac{1}{4}\times1=\frac{1}{4}
$$
对于 $\int_0^1\sqrt{1-x^2}dx$,不能通过矩形分割法近似计算 $\sqrt{1-x^2}$,因为会发现随着分割数增加,误差下降但始终存在(因曲线不可分割为直线段)。所以,我们可以用几何意义简化。容易发现,它表示单位圆 $x^2+y^2=1$ 在第一象限的上半部分,如下图:
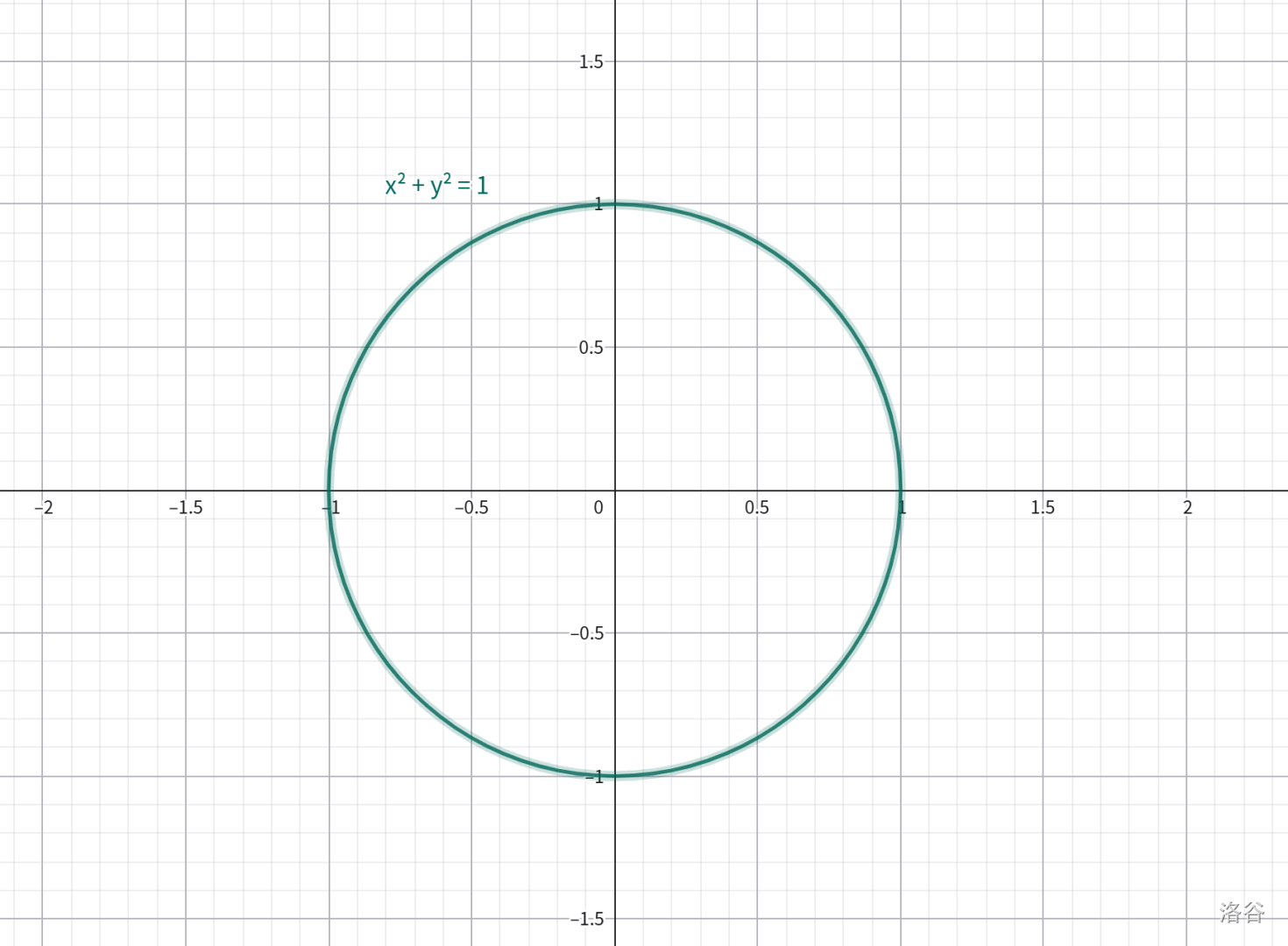
因此积分 $\int_0^1\sqrt{1-x^2}dx$ 就对应四分之一圆的面积(半径为 $1$),即 $\frac{\pi}{4}$。
所以最终结果为:
$$
\frac{1}{4}+\frac{\pi}{4}=\frac{1+\pi}{4}
$$
思考题三:由曲线 $\operatorname{f}(x)=x^3-3x^2+2x$,直线 $x=0$ 和 $x=3$ 以及 $x$ 轴围成的区域面积是多少?
第一步,先求函数 $\operatorname{f}(x)=x^3-3x^2+2x$ 的零点,也就是与 $x$ 轴的交点,要确定在区间 $[0,3]$ 的图形分布情况,如下图:
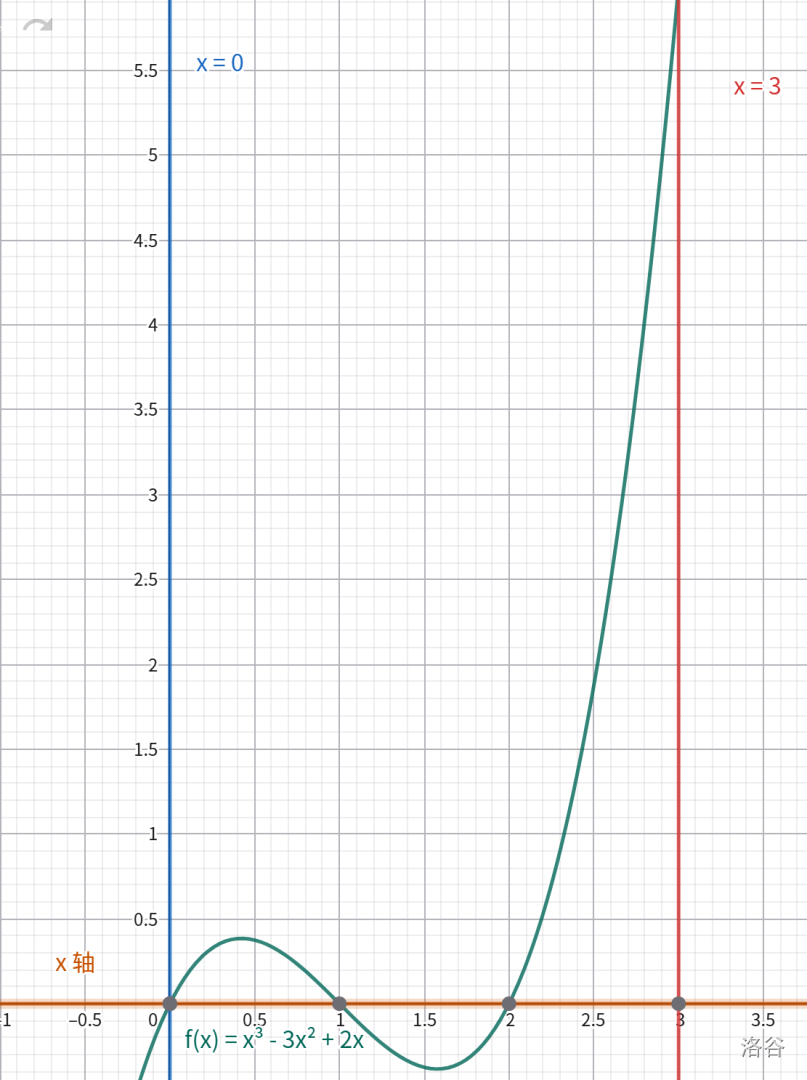
可以发现函数在某些子区间位于 $x$ 轴上方,有些则在下方,所以要分段计算面积,我们把这种计算方式叫做**分段积分**,形式化地讲,若有一个函数 $\operatorname{f}(x)$ 在 $[0,a]$ 上方,$[a,b]$ 下方,则总面积为:
$$
\int_0^a\operatorname{f}(x)dx-\int_a^b\operatorname{f}(x)dx
$$
~~我没有在前面把分段积分当个知识点讲是因为我觉得你们能自己推出来,毕竟洛谷一堆大佬。~~
方法讲完了,直接开始实践。
我们列方程 $x^3-3x^2+2x=0$ 就可以求出零点,三次方程求根公式十分复杂,但我们发现这个式子可以因式分解,所以直接求解即可:
$$
x^3-3x^2+2x=x(x^2-3x+2)=x(x-1)(x-2)
$$
结果十分显然,零点坐标就是 $(0,0)$ 和 $(1,0)$ 和 $(2,0)$。
求完零点后,我们还发现在区间 $[0,3]$ 内,函数 $\operatorname{f}(x)=x^3-3x^2+2x$ 在 $[0,1]$ 和 $[2,3]$ 上方,$[1,2]$ 下方。因此:
$$
\begin{align*}
S&=\int_0^1\operatorname{f}(x)dx-\int_1^2\operatorname{f}(x)dx+\int_2^3\operatorname{f}(x)dx\\
&=\int_0^1(x^3-3x^2+2x)dx-\int_1^2(x^3-3x^2+2x)dx+\int_2^3(x^3-3x^2+2x)dx\\
&=(\frac{1}{4}x^4-x^3+x^2)\bigg|_0^1-(\frac{1}{4}x^4-x^3+x^2)\bigg|_1^2+(\frac{1}{4}x^4-x^3+x^2)\bigg|_2^3\\
&=\frac{1}{4}-(-\frac{1}{4})+\frac{9}{4}\\
&=\frac{11}{4}
\end{align*}
$$
# 扩展:定积分的应用
定积分的思想:分割、近似、求和、取极限”,是求任何连续变化的累积量的万能钥匙。
1. **求体积**:若一个立体介于垂直于 $x$ 轴的两个平面 $x=a$ 与 $x=b$ 之间,且在任意坐标 $x(a\leq x\leq b)$ 处,用垂直于 $x$ 轴的平面去截该立体,所得的截面面积 $\operatorname{A}(x)$ 是已知的,则此立体的体积 $V=\int_a^b\operatorname{A}(x)dx$。并且将一片区域绕轴旋转一周,扫出来的体积也可以用定积分求。例如由曲线 $y=\operatorname{f}(x)$、$x$ 轴、直线 $x=a$ 与 $x=b$ 绕 $x$ 轴旋转,体积 $V=\pi\int_a^b[\operatorname{f}(x)]^2dx$。
2. **求曲线弧长**:一段曲线 $y=\operatorname{f}(x)(a\leq x\leq b)$ 的长度,因为它不是直线,所以我们可以把它分成无数小段,每一小段近似看作直线段,用勾股定理求长,再全部加起来取极限,得到弧长公式:$l=\int_a^b\sqrt{1+[\operatorname{f'}(x)]^2}dx$。
3. **解物理题目**:第一,可以解决变力做功类型的题目。例如对物体施加的力随位置 $x$ 变化而成的函数为 $\operatorname{F}(x)$,力做的总功就是 $W=\int_a^b\operatorname{F}(x)dx$。第二,可以解决液体压力类型的题目。水深不同,水压不同。计算一面竖直浸没于液体中的平板所受的总水压力,由于压强 $p=\rho gh$ 随深度 $h$ 线性增加,因此需要对深度变化的压强沿平板面积进行积分。
此外,定积分还有许多可以用到的地方,因此定积分在生活中具有广泛的应用。
# 结语
恭喜你!成功学会了高中的定积分、极限和求导(当然只是一些基础)!我希望这些内容能够帮助到你,让你彻底理解定积分是什么,这只是起步,由于个人原因,其它的内容只能以后再讲了,我也会努力提升自己,大佬们也可以给一些建议,并且看在我码了一万多字的份上,点个赞再走吧。
补充说明:参考资料为抖音小兀同学和 AI 总结的求导的基本规则,已确保 AI 的贡献严格低于作者。