浅谈欧拉路径
Clare613
·
2025-07-24 11:00:13
·
算法·理论
前言:
本期比较好玩?
何为欧拉路径:
一笔画玩过没有,其实就跟一笔画很相似,就是不重复走路径,走出来的就是欧拉路径,如果起点和终点是同一个点,那么就称为欧拉回路。\
\
如图不是一个欧拉路径,我们可以发现有点 1,2,6,11 这四个点的度数^*为奇数。\
\
这张图就是一个符合的欧拉通路。可以看到只有编号为 1,10 的度数^*为奇数,这两个点就作为起点和终点。所以符合。\
\
像这张图,就是一个欧拉回路。可以发现,所有的点的度数都是偶数,我们给出字典序最小的路径如下:1\rightarrow2\rightarrow3\rightarrow1\rightarrow4\rightarrow5\rightarrow3\rightarrow8\rightarrow5\rightarrow1\rightarrow6\rightarrow2\rightarrow9\rightarrow6\rightarrow7\rightarrow4\rightarrow10\rightarrow7\rightarrow1,图如下:
## 怎么求:
我们可以将欧拉路径抽象成一条线,上面连着多个环,如图:\
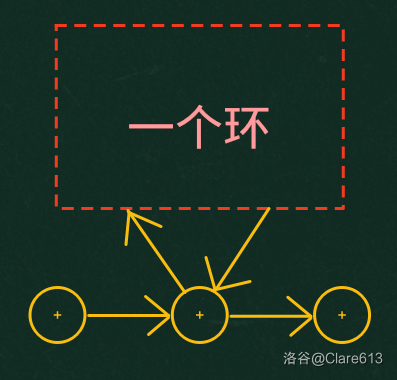\
提出求欧拉路径方法的人是 $\tt {Heirholzer|希尔霍尔策}$,代码如下:
```cpp
void dfs(int u){
for(int i=0;i if(vis[u][i]==0){ vis[u][i]=1; dfs(g[u][i]); } } ans.push_back(u); } ``` 但是面对数据量较大的题,这个方法就不占优势了。我们可以运用弧优化(又名删边优化),就是记录走过的边,这样就不用花大量的时间来记录和判断走过的边了,代码如下: ```cpp void dfs(int u){ for(int i=head[u];i head[u]=i+1; dfs(g[u][i]); } ans.push_back(u); } ``` ## 例题: 本期的例题分两种:欧拉路径题和欧拉路径性质题。[题单](https://www.luogu.com.cn/training/811622#problems)。 ### P7771 【模板】欧拉路径: 模板题,没得说。 ```cpp #include using namespace std; vector int head[1000006]; void dfs(int u){ for(int i=head[u];i head[u]=i+1; dfs(g[u][i]); } ans.push_back(u); } int in[100005],out[100005]; int main(){ int n,m; cin>>n>>m; for(int i=1;i<=m;i++){ int u,v; cin>>u>>v; g[u].push_back(v); in[v]++; out[u]++; } int c1=0,c2=0,id=1; for(int i=1;i<=n;i++){ if(out[i]-in[i]==1){ c1++; id=i; } if(in[i]-out[i]==1){ c2++; } } for(int i=1;i<=n;i++) sort(g[i].begin(),g[i].end()); if((c1==0&&c2==0)==0&&(c1==1&&c2==1)==0){ cout<<"No\n"; return 0; } dfs(id); for(int i=ans.size()-1;i>=0;i--) cout< return 0; } ``` ### P1341 无序字母对: 字母型的欧拉路径,好像没有难点。 ```cpp #include #define int long long using namespace std; int g[105][105]; vector int du[105],head[105]; void dfs(int u){ for(int i=head[u];i<100;i=head[u]){ head[u]=i+1; if(g[u][i]==1){ g[u][i]=g[i][u]=0; dfs(i); } } ans.push_back(u); } signed main(){ cin.tie(0)->sync_with_stdio(0); cout.tie(0)->sync_with_stdio(0); int n,minn=1e9; cin>>n; for(int i=1;i<=n;i++){ char x,y; cin>>x>>y; g[x-'A'][y-'A']=g[y-'A'][x-'A']=1; du[x-'A']++;du[y-'A']++; } int id=0; for(int i=0;i<100;i++){ if(du[i]%2==1){ id=i; break; } } if(id==0){ for(int i=0;i<100;i++){ if(du[i]!=0){ id=i; break; } } } dfs(id); if(ans.size()!=n+1){ cout<<"No Solution"; return 0; } else if(ans[ans.size()-2]=='f'-'A'){ cout<<"No Solution"; return 0; } for(int i=ans.size()-1;i>=0;i--){ cout< } return 0; } /* abaaba */ ``` ### P1333 瑞瑞的木棍: 欧拉路径性质题,只需要用并查集判断是否连通和度数为奇数的点的个数即可。 ```cpp #include using namespace std; map map string find(string x){ if(fa[x]==x) return x; return fa[x]=find(fa[x]); } int cnt=0,ctn=0,fl=0; int main(){ string x,y; while(cin>>x>>y){ if(fa[x]==""){ fa[x]=x; cnt++; } if(fa[y]==""){ fa[y]=y; cnt++; } if(mp[x]%2==0) fl++; else fl--; mp[x]++; if(mp[y]%2==0) fl++; else fl--; mp[y]++; if(find(x)!=find(y)){ ctn++; fa[find(x)]=find(y); } } if((fl!=0&&fl!=2)||(cnt!=0&&ctn!=cnt-1)) cout<<"Impossible"; else cout<<"Possible"; return 0; } ``` ### P3520 [POI 2011] SMI-Garbage: 这道题目是无向图,需要使用链式前项星,然后对于需要反转的边,标记一下,然后分成连通块跑完。 ```cpp #include using namespace std; int n,m; int head[2000006]; struct node{ int v,w,nxt; }edge[2000005]; int du[2000005]; bool f[2000005]; bool ff[2000005]; vector int cnt=0; void ae(int u,int v,int w){ edge[++cnt]={v,w,head[u]}; head[u]=cnt; return ; } int ans=0; stack int is[2000005]; void dfs(int u){ f[u]=1; for(int i=head[u];i;i=head[u]){ head[u]=edge[i].nxt; if(ff[i]) continue; ff[i]=ff[i^1]=1; int v=edge[i].v; dfs(v); if(is[v]){ g[++ans].push_back(v); while(st.top()!=v){ g[ans].push_back(st.top()); is[st.top()]=0; st.pop(); } g[ans].push_back(v); } else{ st.push(v); is[v]=1; } } } signed main(){ cin.tie(0)->sync_with_stdio(0); cout.tie(0)->sync_with_stdio(0); cin>>n>>m; cnt=1; while(m--){ int u,v,x,y; cin>>u>>v>>x>>y; if(x^y){ ae(u,v,0); ae(v,u,0); du[u]++; du[v]++; } } for(int i=1;i<=n;i++){ if(du[i]%2){ cout<<"NIE"; return 0; } } for(int i=1;i<=n;i++){ if(!f[i]&&du[i]){ dfs(i); g[++ans].push_back(i); while(st.size()){ g[ans].push_back(st.top()); is[st.top()]=0; st.pop(); } } } cout< for(int i=1;i<=ans;i++){ int len=g[i].size(); cout< for(int j=0;j cout< } cout<<"\n"; } return 0; } ``` ### P10777 BZOJ3706 反色刷: 又是一道性质题。我们需要对于每次修改来处理并查集,然后对于不同的连通块,我们需要排查个数及是否可行即可。 ```cpp #include using namespace std; int n,m,fa[1000005]; int du[1000005]; int siz[1000005]; int u[1000005]; int v[1000005]; int w[1000005]; int cnt=0; int find(int x){ if(fa[x]==x) return x; return fa[x]=find(fa[x]); } void uni(int x,int y){ x=find(x); y=find(y); if(x!=y){ fa[x]=y; } return ; } void solve(int x,int y){ if(du[x]){ cnt++; } else{ cnt--; } du[x]^=1; if(du[y]){ cnt++; } else{ cnt--; } du[y]^=1; } int main(){ cin.tie(0)->sync_with_stdio(0); cout.tie(0)->sync_with_stdio(0); cin>>n>>m; for(int i=1;i<=n;i++){ fa[i]=i; } for(int i=1;i<=m;i++){ cin>>u[i]>>v[i]>>w[i]; if(w[i]){ solve(u[i],v[i]); } uni(u[i],v[i]); } int e=0; for(int i=1;i<=m;i++){ if(w[i]){ int ro=find(u[i]); if(!siz[ro]){ e++; } siz[ro]++; } } int q; cin>>q; while(q--){ int op; cin>>op; if(op==2){ if(cnt){ cout<<"-1\n"; } else{ cout< } } else{ int x; cin>>x; x++; solve(u[x],v[x]); int ro=find(u[x]); if(w[x]){ w[x]=0; siz[ro]--; if(!siz[ro]){ e--; } } else{ w[x]=1; if(!siz[ro]){ e++; } siz[ro]++; } } } return 0; } ``` ## 后话: 小小欧拉路径,拿捏。